Let us begin at the beginning with Newton who said that action and reaction are equal and opposite. This means that every push must be matched and balanced by an equal and opposite push. It does not matter how the push arises. It may be a ‘dead’ load for instance: that is to say a stationary weight of some kind. If I weigh 200 pounds and stand on the floor, then the soles of my feet push downwards on the floor with a push or thrust of 200 pounds: that is the business of feet. At the same time the floor must push upwards on my feet with a thrust of 200 pounds: that is the business of floors. If the floor is rotten and cannot furnish a thrust of 200 pounds then I shall fall through the floor. If, however, by some miracle, the floor produced a larger thrust than my feet have called upon it to produce, say 201 pounds, then the result would be still more surprising because, of course, I should become airborne.
(J. E. Gordon 1991, p.28)
Newton’s third law of motion is that action and reaction are always equal and always opposite in direction. In other words, if your feet push down on the floor then the floor must push up on your feet with equal force of support. See Khan Academy for a more entertaining description of Newton’s third law of motion.
The point at which a body’s weight balances equally in all directions is the center of gravity. The total weight of an object is concentrated at this point. Our total weight from the center of gravity does not travel downwards through the skeleton, i.e. it does not spread down and across structures. Gravity pulls our weight downwards in a straight line directly to the center of the earth. The line of gravity at the earth’s surface is more or less 90° to the surface.
Our weight is due to gravity. Without gravity we would have no weight, i.e. we would be weightless. Gravity is a field force: it doesn’t change; the pull of gravity remains the same whether you have your feet on the ground or not. Newton described gravity as ‘The Universal Constant’ and it has an effect on our bones and joints and activates our upwards supporting reaction in response.
Ground Reaction Force (no, not a gardening program)
The supporting reaction force of the earth is equal and opposite of our weight. The difference between the supporting force and the force due to gravity is that the supporting force is a contact force; there has to be physical contact in order for a supporting reaction to take place. Gravity, on the other hand, is a field force and is unchanging; it remains the same whether there is contact or not. It is necessary that our body’s structure (skeleton) have actual physical contacts, such as that between the feet and the ground, in order for the reaction of support to happen.
This supporting force transfers from the earth’s surface and supports our weight. It transmits through the bones of the feet to the bones that are not in direct contact with the support of the ground. Ground reaction force travels through the bones of the feet through the bones of the ankle joint to the bones of the lower leg. In the lower leg, this force is conducted upward principally through the tibia to the knee joint and through to the femur. At the top of the femur, it travels inwards through the hip joints at roughly 70° to the vertical, around the inner rim of the pelvis to the sacroiliac joint. The support force continues from the sacroiliac joint through the ‘front ledge’ of the sacrum to the front of the lumbar spine. The bodies of the vertebrae conduct the force upward at the front of the spine – more or less in the middle of the torso. It continues to travel through the curves of the spine, upwards through the thoracic vertebrae and the cervical vertebrae to support the skull at the atlantooccipital joint. The head is supported from underneath by the cervical spine in a balance that Alexander Teachers describe as forward and upward.
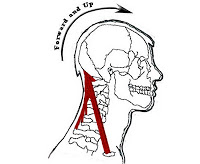
The joints of the body connect the bones together and allow them to move. Ligaments and muscles keep the joints stable. The supporting force travels through joints so that each skeletal section fully supports the part of the skeleton that is directly above it and in contact with it.